Multiple Choice Answer and Explanations with Advice and Hints...
remember the concepts!
1) f '(x) = 3x^2 - 6x = 3x (x - 2)
Only critical numbers of f occur when f '(x)=0, that is, x=0 or x=2. These critical numbers are in the interval ( -1/2, 4)
The values of f at these critical numbers are f(0)=1 and f(2)= -3. Also, f(-1/2) = 1/8 and f(4) = 17.
comparing these four numbers we get absolute max is f(4) = 17 and abs min is f(2) = -3
ANSWER IS C
** Remember how to do the first derivative test for absolute extrema!
2) Maximize: A=xy
Constraint: 500 = x + 2yThe area function (as well as the constraint) has two variables in it and so what we know about finding absolute extrema won’t work. However, if we solve the constraint for one of the two variables we can substitute this into the area and we will then have a function of a single variable.
x= 500 - 2y then substitute into area: A(y) = (500 - 2y)y = 500y - y^2 then find the derivative and the critical pointsA'(y) = 500 - 4yset equal to zero and you get y = 125.then get x by plugging y value into constraint function and you get x= 250
ANSWER IS A
3) dimensions H x W x L = H x W x 3W
C=10(2LW)+6(2WH+2LH)=60W^2+48WH
Solve for H.....H= 50/(3W^2)
plug into cost then find the second derivative.
C'(W)= (120W^3 - 800)/W^2
C''(W)=120+1600W^(-3)
two critical points at W=0 and where numerator is 0.
W=1.8821
then find remaining conditions: L=3W=5.6463 & H=50/(3W^2)=4.7050
ANSWER IS A
4) similarly to #3, find relations and use the derivative tests to find the MINIMUM for cost and/or plug in found mininum dimensions into the cost equation.
ANSWER IS B
5) distance between the point (1,4) and (x,y) is d=sqrt[(x-1)^2 + (y-4)^2]. But if (x,y) lies on the parabola, then x=(y^2)/2 so d=sqrt[(.5y^2-1)^2 + (y-4)^2]
instead of minimizing d, we minimize its square: d^2=f(y)=(.5y^2-1)^2+(y-4)^2
differentiate and get: f '(y)= y^3 - 8
so f '(y)=0 when y=2. using first derivative test for absolute extreme values, the absolute minimum occurs when y=2. X=y^2/2=2. So the point on y^2=2x closest to (1,4) is (2,2)
ANSWER IS D
6) The upper half of the circle can be x^2 + y^2=r^2with the center as the origin. If (x,y) is the vertex that lies in the first quadrant, then the rectangle has sides of lengths 2x and y so the area is A=2xy
y=sqrt(r^2 - x^2) and A=2x[sqrt(r^2 - x^2)]
the derivative is A'= 2[sqrt(r^2 - x^2)] - (2x^2)/sqrt(r^2 - x^2)= (2(r^2-2x^2))/sqrt(r^2 - x^2) with the domain 0</= x </= r
A' is 0 when 2x^2 is r^2. this gives value of maximum since A(0) = 0 and A(r) = 0. therefore the area of the largest inscribed rectangle is
A(r/(sqrt(2))) = r^2
ANSWER IS B
7)Let distance BP be equal to x. Let us find a formula for the distances AP and PC. Using Pythagorean theorm, we can write:
distance AP = sqrt(5 2 + x 2)distance PC = 10 - xWe now find time t 1 to walk distance AP.(time = distance / speed).
t 1 = distance AP / 3 = sqrt(5 2 + x 2) / 3Time t 2 to walk distance PC is given by
t 2 = distance PC / 5 = (10 - x) / 5The total time t is found by adding t 1 and t 2.
t = sqrt(5 2 + x 2) / 3 + (10 - x) / 5
we might consider the domain of function t as being all values of x in the closed interval [0 , 10]. For values of x such that point P is to the left of B or to the right of c, time t will increase.
To find the value of x that gives t minimum, we need to find the first derivative dt/dx (t is a functions of x).
dt/dx = (x/3) / sqrt(5 2 + x 2) - 1/5
If t has a minimum value, it happens at x such that dt/dx = 0.
(x/3) / sqrt(5 2 + x 2) - 1/5 = 0
Solve the above for x. Rewrite the equation as follows.
5x = 3sqrt(5 2 + x 2)
Square both sides.
25x 2 = 9(5 2 + x 2)
Group like terms and simplify
16x 2 = 225
Solve for x (x >0 )
x = sqrt(225/16) = 3.75 km.
conduct a derivative testThe first derivative dt/dx is negative for x < 3.75, equal to zero at x = 3.75 and positive for x >3.75. Also the values of t at x = 0 and x = 10 (the endpoints of the domain of t) are respectively 3.6 hrs and 3.7 hrs. The value of t at x = 3.75 is equal to 3.3 hrs and its is the smallest. The answer to our problem is that one has to walk to point P such BP = 3.75 km then procced along the road to C in order to get there in the shortest possible time.
ANSWER IS D
8)The height of the rectangular portion is h and because the semicircle is on top we can think of the width of the rectangular portion at 2r. The perimeter (our constraint) is the lengths of the three sides on the rectangular portion plus half the circumference of a circle of radius r. The area (what we want to maximize) is the area of the rectangle plus half the area of a circle of radius r.
Maximize: A=2hr+.5(pi)r^2
constraint: 12=2h+2r+(pi)r
solve for h in constraint and plug into the Area equation
then take the derivatives. you get: A'(r)= 12 - r(4+pi) and A"(r)= -4 - pi
the only critical point is r=12/(4+pi)=1.6803. So, for the maximum area the semicircle on top must have a radius of 1.6803 and the rectangle must have the dimensions 3.3606 x 1.6803 (h x 2r).
ANSWER IS B
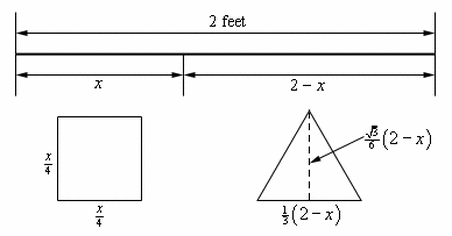
9) remember! an equilateral triangle is a triangle with three equal sides and each of the interior angles are 60 degrees.Now, this is another problem where the constraint isn’t really going to be given by an equation, it is simply that there is 2 ft of wire to work with and this will be taken into account in our work.
So, let’s cut the wire into two pieces. The first piece will have length x which we’ll bend into a square and each side will have length x/4 . The second piece will then have length (2 - x) (we just used the constraint here…) and we’ll bend this into an equilateral triangle and each side will have length (2 - x)/3
Only critical numbers of f occur when f '(x)=0, that is, x=0 or x=2. These critical numbers are in the interval ( -1/2, 4)
The values of f at these critical numbers are f(0)=1 and f(2)= -3. Also, f(-1/2) = 1/8 and f(4) = 17.
comparing these four numbers we get absolute max is f(4) = 17 and abs min is f(2) = -3
ANSWER IS C
** Remember how to do the first derivative test for absolute extrema!
2) Maximize: A=xy
Constraint: 500 = x + 2yThe area function (as well as the constraint) has two variables in it and so what we know about finding absolute extrema won’t work. However, if we solve the constraint for one of the two variables we can substitute this into the area and we will then have a function of a single variable.
x= 500 - 2y then substitute into area: A(y) = (500 - 2y)y = 500y - y^2 then find the derivative and the critical pointsA'(y) = 500 - 4yset equal to zero and you get y = 125.then get x by plugging y value into constraint function and you get x= 250
ANSWER IS A
3) dimensions H x W x L = H x W x 3W
C=10(2LW)+6(2WH+2LH)=60W^2+48WH
Solve for H.....H= 50/(3W^2)
plug into cost then find the second derivative.
C'(W)= (120W^3 - 800)/W^2
C''(W)=120+1600W^(-3)
two critical points at W=0 and where numerator is 0.
W=1.8821
then find remaining conditions: L=3W=5.6463 & H=50/(3W^2)=4.7050
ANSWER IS A
4) similarly to #3, find relations and use the derivative tests to find the MINIMUM for cost and/or plug in found mininum dimensions into the cost equation.
ANSWER IS B
5) distance between the point (1,4) and (x,y) is d=sqrt[(x-1)^2 + (y-4)^2]. But if (x,y) lies on the parabola, then x=(y^2)/2 so d=sqrt[(.5y^2-1)^2 + (y-4)^2]
instead of minimizing d, we minimize its square: d^2=f(y)=(.5y^2-1)^2+(y-4)^2
differentiate and get: f '(y)= y^3 - 8
so f '(y)=0 when y=2. using first derivative test for absolute extreme values, the absolute minimum occurs when y=2. X=y^2/2=2. So the point on y^2=2x closest to (1,4) is (2,2)
ANSWER IS D
6) The upper half of the circle can be x^2 + y^2=r^2with the center as the origin. If (x,y) is the vertex that lies in the first quadrant, then the rectangle has sides of lengths 2x and y so the area is A=2xy
y=sqrt(r^2 - x^2) and A=2x[sqrt(r^2 - x^2)]
the derivative is A'= 2[sqrt(r^2 - x^2)] - (2x^2)/sqrt(r^2 - x^2)= (2(r^2-2x^2))/sqrt(r^2 - x^2) with the domain 0</= x </= r
A' is 0 when 2x^2 is r^2. this gives value of maximum since A(0) = 0 and A(r) = 0. therefore the area of the largest inscribed rectangle is
A(r/(sqrt(2))) = r^2
ANSWER IS B
7)Let distance BP be equal to x. Let us find a formula for the distances AP and PC. Using Pythagorean theorm, we can write:
distance AP = sqrt(5 2 + x 2)distance PC = 10 - xWe now find time t 1 to walk distance AP.(time = distance / speed).
t 1 = distance AP / 3 = sqrt(5 2 + x 2) / 3Time t 2 to walk distance PC is given by
t 2 = distance PC / 5 = (10 - x) / 5The total time t is found by adding t 1 and t 2.
t = sqrt(5 2 + x 2) / 3 + (10 - x) / 5
we might consider the domain of function t as being all values of x in the closed interval [0 , 10]. For values of x such that point P is to the left of B or to the right of c, time t will increase.
To find the value of x that gives t minimum, we need to find the first derivative dt/dx (t is a functions of x).
dt/dx = (x/3) / sqrt(5 2 + x 2) - 1/5
If t has a minimum value, it happens at x such that dt/dx = 0.
(x/3) / sqrt(5 2 + x 2) - 1/5 = 0
Solve the above for x. Rewrite the equation as follows.
5x = 3sqrt(5 2 + x 2)
Square both sides.
25x 2 = 9(5 2 + x 2)
Group like terms and simplify
16x 2 = 225
Solve for x (x >0 )
x = sqrt(225/16) = 3.75 km.
conduct a derivative testThe first derivative dt/dx is negative for x < 3.75, equal to zero at x = 3.75 and positive for x >3.75. Also the values of t at x = 0 and x = 10 (the endpoints of the domain of t) are respectively 3.6 hrs and 3.7 hrs. The value of t at x = 3.75 is equal to 3.3 hrs and its is the smallest. The answer to our problem is that one has to walk to point P such BP = 3.75 km then procced along the road to C in order to get there in the shortest possible time.
ANSWER IS D
8)The height of the rectangular portion is h and because the semicircle is on top we can think of the width of the rectangular portion at 2r. The perimeter (our constraint) is the lengths of the three sides on the rectangular portion plus half the circumference of a circle of radius r. The area (what we want to maximize) is the area of the rectangle plus half the area of a circle of radius r.
Maximize: A=2hr+.5(pi)r^2
constraint: 12=2h+2r+(pi)r
solve for h in constraint and plug into the Area equation
then take the derivatives. you get: A'(r)= 12 - r(4+pi) and A"(r)= -4 - pi
the only critical point is r=12/(4+pi)=1.6803. So, for the maximum area the semicircle on top must have a radius of 1.6803 and the rectangle must have the dimensions 3.3606 x 1.6803 (h x 2r).
ANSWER IS B
9) remember! an equilateral triangle is a triangle with three equal sides and each of the interior angles are 60 degrees.Now, this is another problem where the constraint isn’t really going to be given by an equation, it is simply that there is 2 ft of wire to work with and this will be taken into account in our work.
So, let’s cut the wire into two pieces. The first piece will have length x which we’ll bend into a square and each side will have length x/4 . The second piece will then have length (2 - x) (we just used the constraint here…) and we’ll bend this into an equilateral triangle and each side will have length (2 - x)/3
find the height of the triangle using sin(pi/3)= opp/hyp, opp = (sqrt(3)/6)(2 - x)
so the total area is A= x^2/16 + (sqrt3)/36(2 - x)^2
Take the first derivative: x/8 - sqrt(3)/9 + xsqrt(3)/18
set equal to zero and you get critical point of x = 0.8699
conduct derivative test and verify 0.8699 is the distance for minimum enclosed area
ANSWER IS A
10) Let’s notice that x must be in the range x </= x </= 2A(0) and since the area function is continuous we use the basic process for finding absolute extrema of a function.
A(0) = 0.1925 A(0.8699)=0.1087 A(2)=0.25the maximum area will arise if we take the whole piece of wire and bend it into a square
ANSWER IS C
so the total area is A= x^2/16 + (sqrt3)/36(2 - x)^2
Take the first derivative: x/8 - sqrt(3)/9 + xsqrt(3)/18
set equal to zero and you get critical point of x = 0.8699
conduct derivative test and verify 0.8699 is the distance for minimum enclosed area
ANSWER IS A
10) Let’s notice that x must be in the range x </= x </= 2A(0) and since the area function is continuous we use the basic process for finding absolute extrema of a function.
A(0) = 0.1925 A(0.8699)=0.1087 A(2)=0.25the maximum area will arise if we take the whole piece of wire and bend it into a square
ANSWER IS C